För att lösa ekvationer av typen \cos x = k, där -1 \leq k \leq 1 så gör vi på ett liknande vis som typen sinx = k och även här är det bra att känna till enhetscirkeln och sambanden i denna cirkel.

Vi tittar först på följande bild.

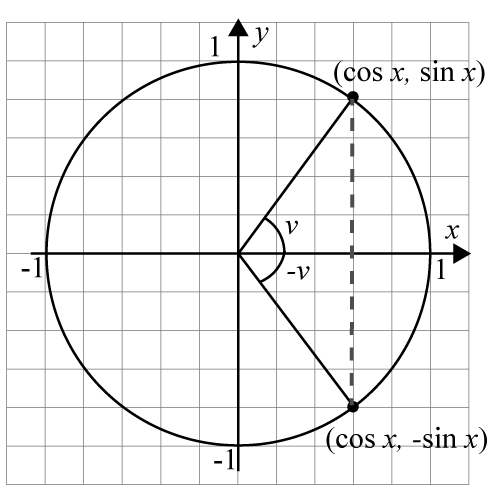
Ur bilden kan vi utläsa att \cos v = \cos(-v) då dessa två punkter på enhetscirkeln har samma x-värde. Dessa två punkter kommer även återkomma oändligt många gånger om vi låter v snurra ett eller flera varv och komma tillbaka till punkten igen.

Följande lösningar gäller därför för en ekvation\cos x = k, där -1 \leq k \leq 1

x=\pm v+n \cdot 360^{\circ}\,\text{där n är ett heltal}

Exempel på lösning av en trigonometrisk ekvation

Lös ekvationen

2 \cos x = 0,8

Dela bägge leden med 2

\cos x = 0,4

Cosinusinvers ger

x=\pm \arccos(0,4) + n \cdot 360^{\circ} \\
x=\pm 66,4^{\circ} + n \cdot 360^{\circ} 

Dessa är den fullständiga (dvs alla lösningar) till ekvationen.

Exempel 2

Nu löser vi en annan typ av ekvation som kan dyka upp. Notera gärna att de första stegen här skulle göras på samma vis som om du exempelvis skulle ha sinus istället i ekvationen. Därefter är det förstås viktigt att du använder metoden för sinus istället.

Lös den trigonometriska ekvationen

4 - 2 \cos x = 4,8

Vi subtraherar med 4 i bägge leden

-2\cos x = 0,8

Dela bägge leden med -2

cos x = -0,4

Cosinusinvers ger

x=\pm \arccos(-0,4) + n \cdot 360^{\circ} \\
x=\pm 113,6^{\circ} + n \cdot 360^{\circ} 

Dessa är den fullständiga (dvs alla lösningar) till ekvationen.